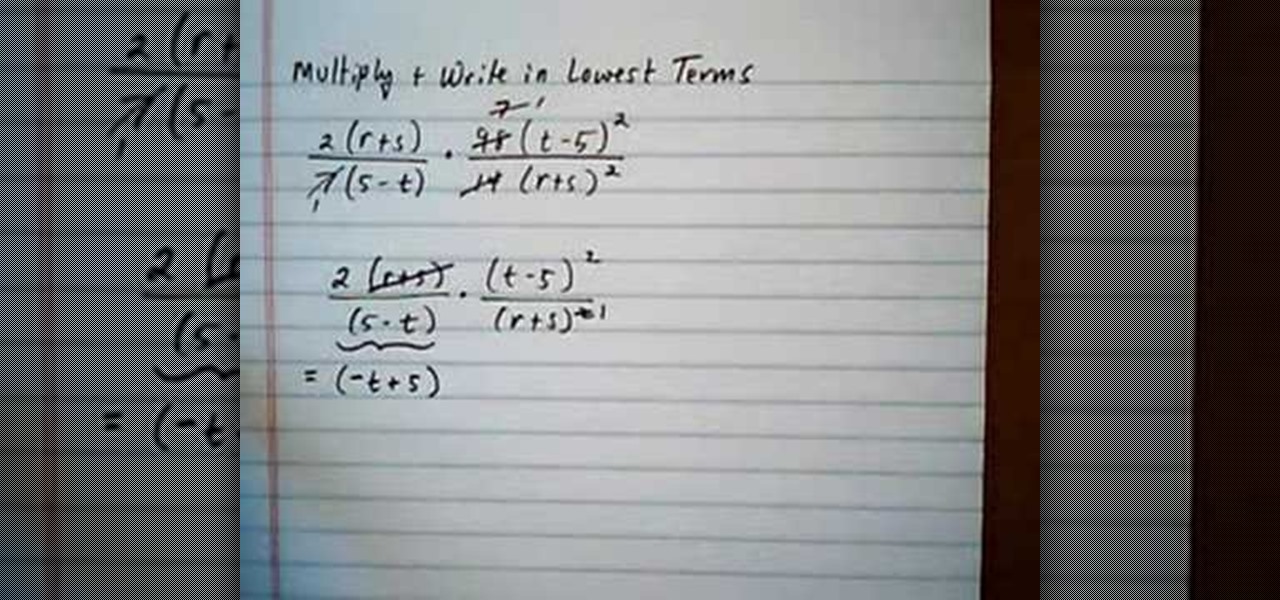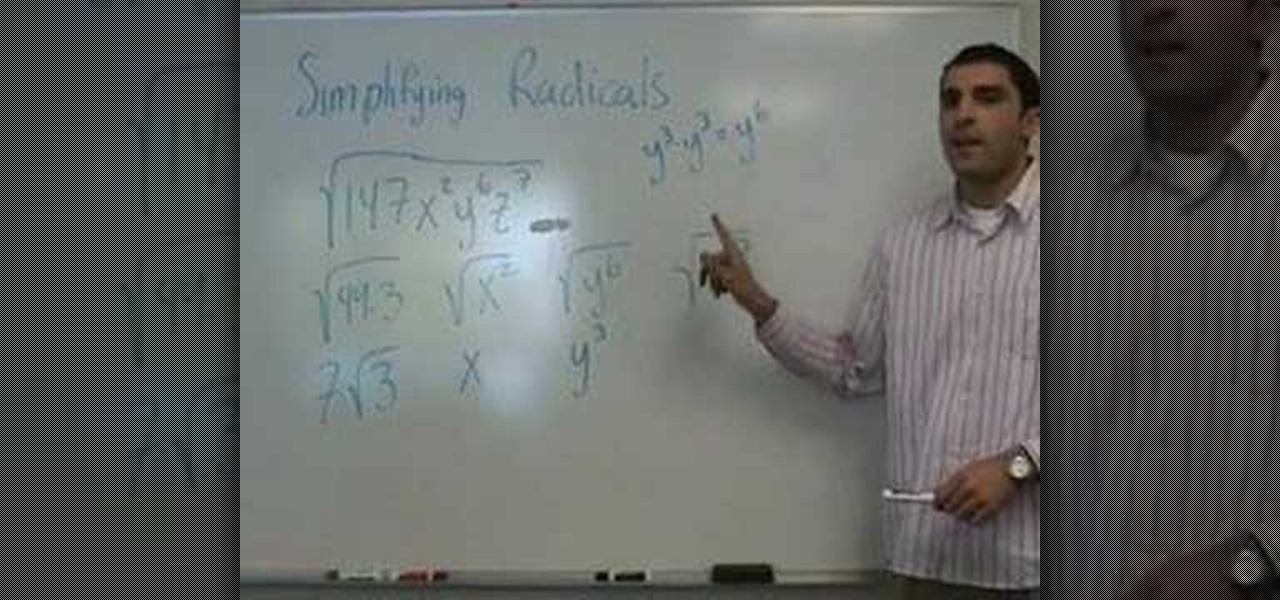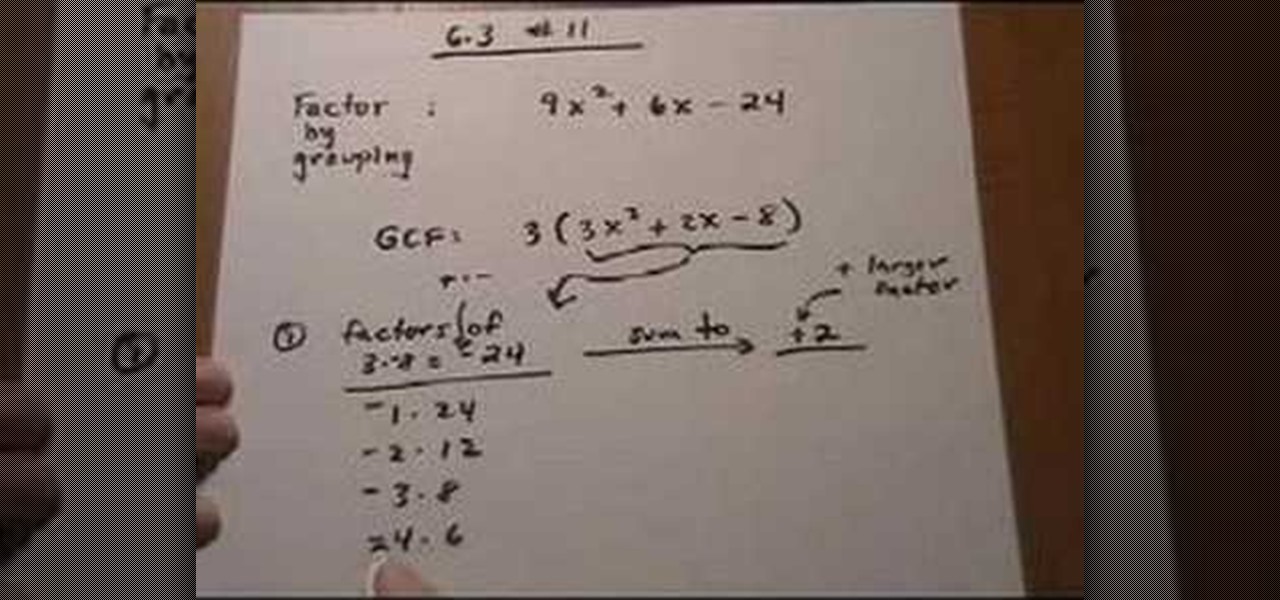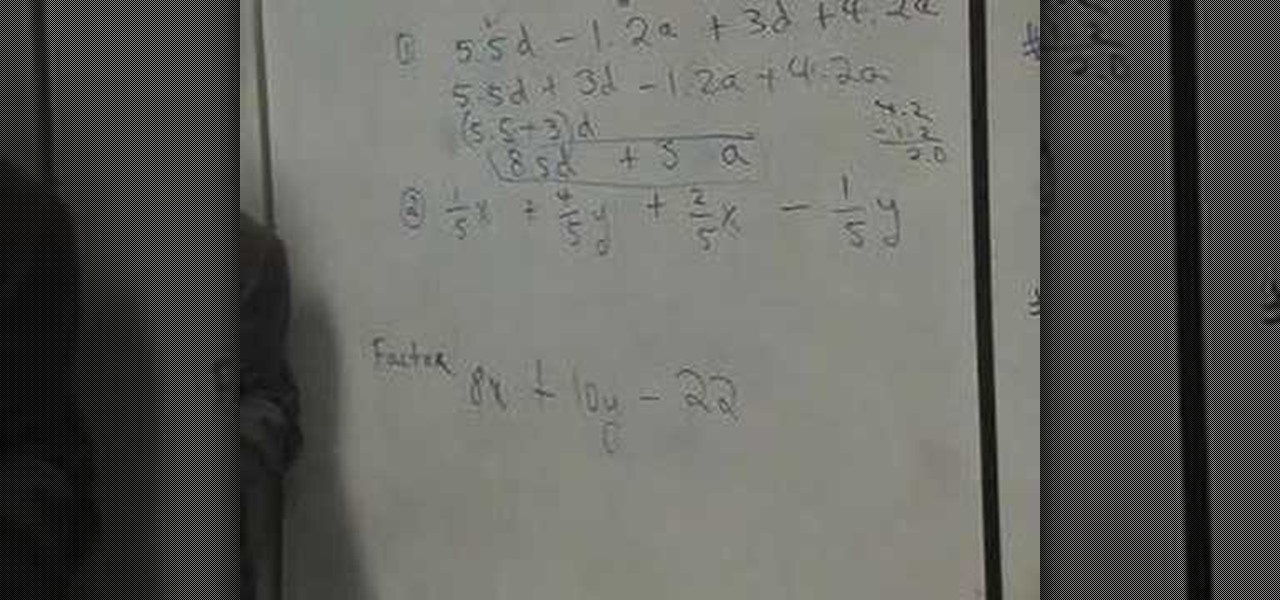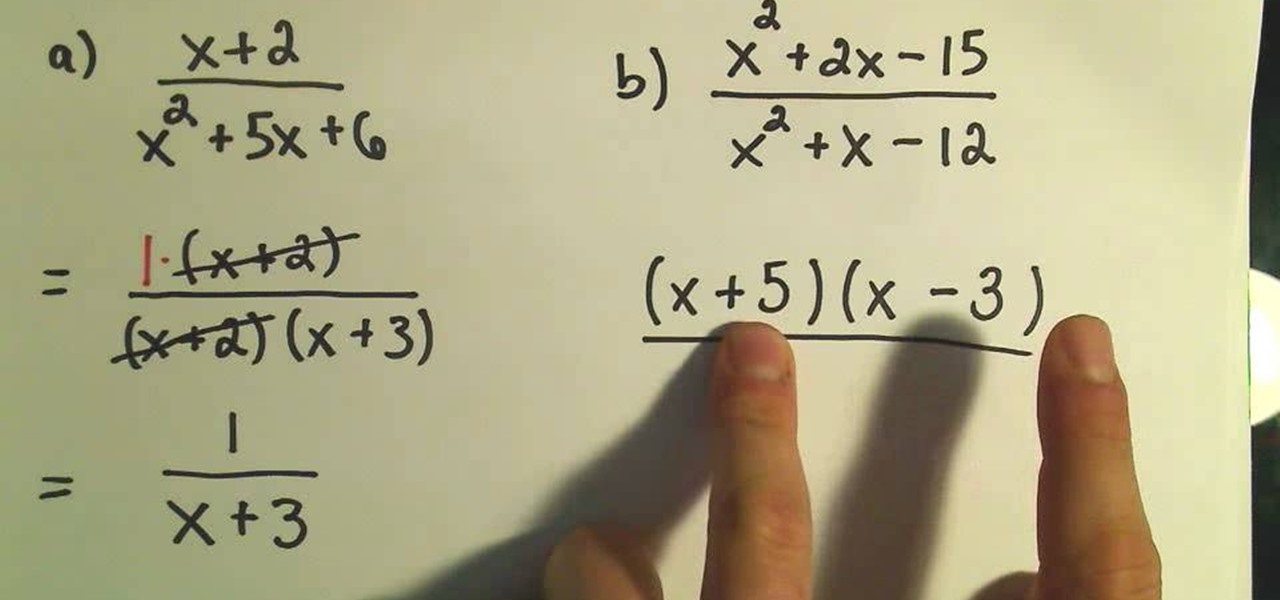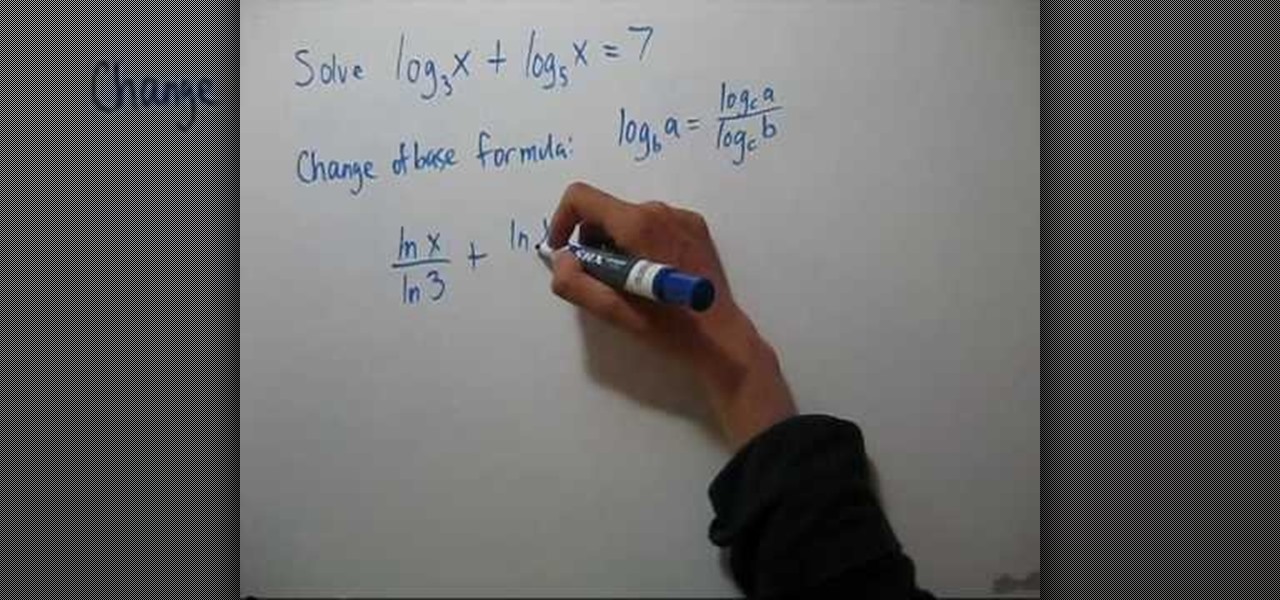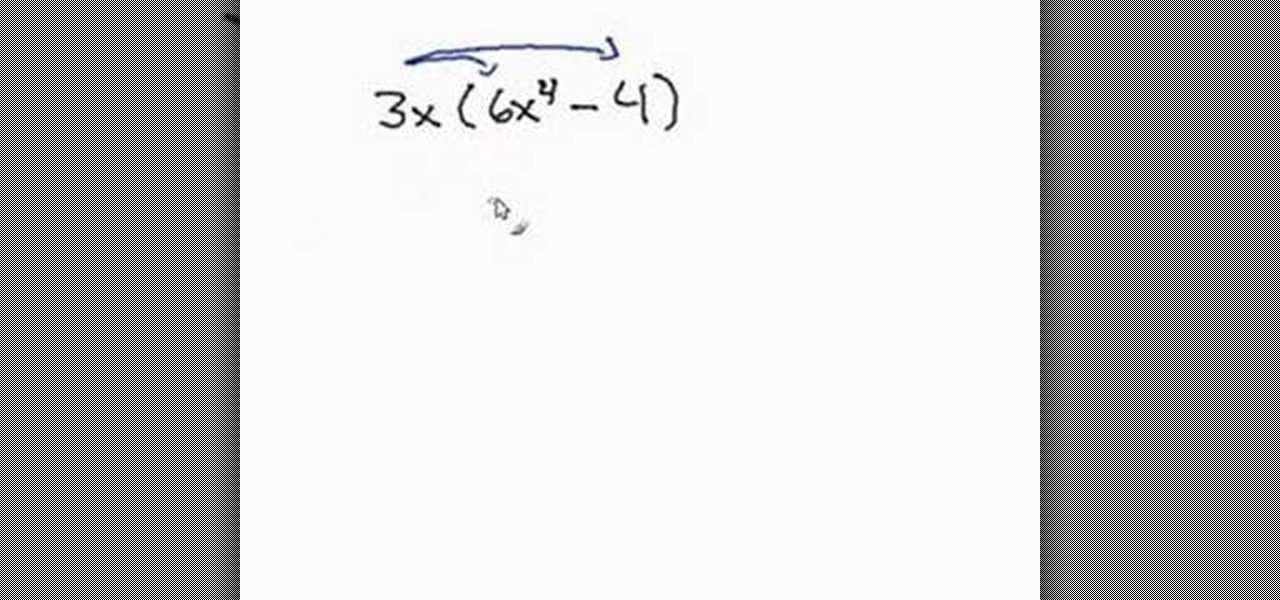
Need some high quality images to work on? High resolution images are those that are at least 300 dpi (dots per inch)... In layman's terms, high quality. When an image is less than 300 dpi, you will notice a loss in quality and an add-in of pixelation when printed.

How to make that cardboard hood to assist you in making your own custom bokeh when shooting images.
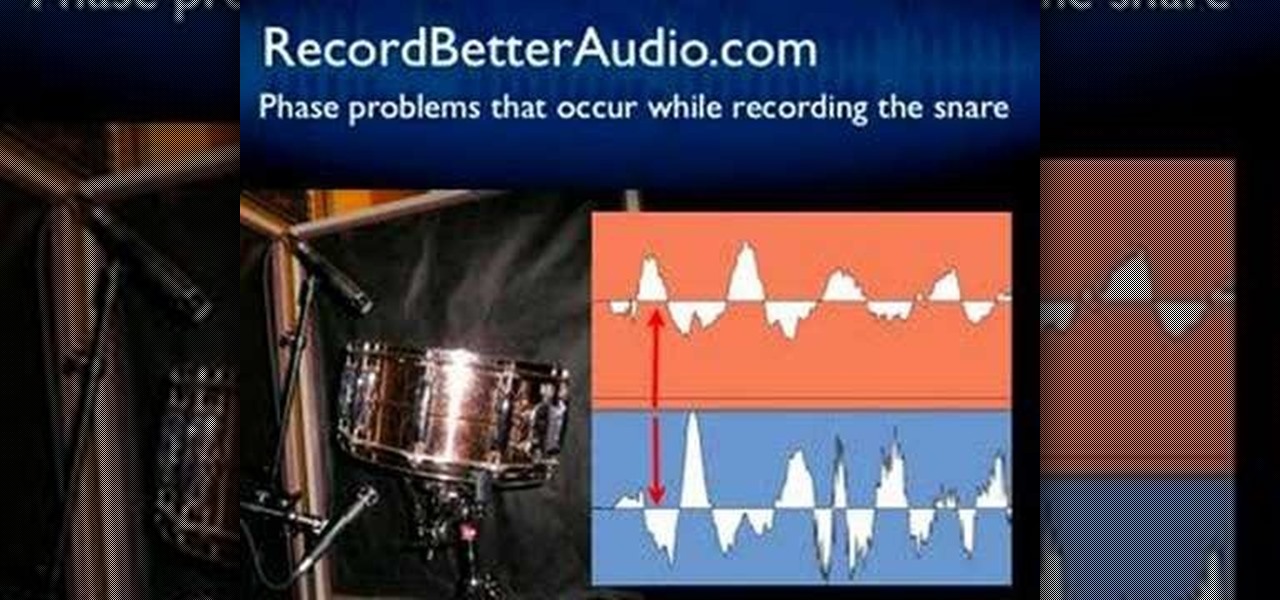
You might have heard the term "phase" before, but do you know what it is? Check out this instructional recording video that demonstrates how to avoid a phase. Hear some audio examples and learn to listen for a phase. Record better sound quality by learning a few tricks outlined in this tutorial video.

Have you ever heard the expression "Dress for Success" or "Clothes Make the Man"? When you're wearing a perfectly fitted designer shirt, something inside just shouts, "I look good" and when you genuinely think that, those feeling are radiated outward to all your come in contact with. That said, what kind of designer shirt are you interested in, a bargain basement discount, or one tailored made, outlining your best features?

To solve simple algebraic expressions you have to use different properties. Distributive property is one among them. To apply distributive property in a algebraic expression multiply each term inside the parenthesis by the outside term. In this way you are distributing the outside term to all the inside terms and removing the parenthesis. Hence it is called distributive property. After multiplying add the like terms to simplify it further. Care should be taken to ensure the proper sign change...

Consider this Beading 101. In this video, you'll learn the five basic beading terms used in many beading magazines and beading patterns. These terms refer to how you pass needles through your beeds (from the back or from the front), how you separate irregular beads out of your main beading inventory, rounds and rows (different ways of beading), waxing your thread, and thread tension.

This two-part chess lesson will get you up to date on the opening terms of the game, along with the positional concepts. This is perfect if you are in need of perfecting your skills.

In this video the instructor shows how to factor a general quadratic polynomial. Here the first step is to identify the coefficient of the squared term. Write the reciprocal of the numerical coefficient of the squared term out side and write two separate parenthesis which are going to contain the binomials which are the factors of the original equation. The first term of both the binomials is the first term numerical coefficient times the unknown variable. Now multiply the first term numerica...

In this video the instructor shows how to multiply and write rational expressions in lowest terms. The fist thing you need to do is cancel out the common factors in the numerator and the denominator. You can cancel a term in the top with a term in the bottom even if they are diagonal as long as one is in numerator and the other is in the denominator. After cancellation if you have a term in numerator and an identical term in the denominator but with opposite signs, then pull out the negative ...

In this tutorial the instructor shows how to identify similar terms in a polynomial equation. He states that in similar terms the variables and their exponents are exactly the same but they may differ in the co-efficient. He shows how to identify similar terms by using some examples. He shows that a change is even the co-efficient makes them dissimilar terms. Similar terms can be further added as the variable of both the terms is same. This video gives an idea of what similar terms are and ho...

If you want to go from a Rookie Cook to an All Star, you must understand the cooking terms. And if you think blanch is just a character from "The Golden Girls," then this episode is for you. Follow along with this cooking how to video to understand basic cooking terms.

Factorization of a trinomial can be achieved by using the standard method of appropriately "splitting the middle term" or by this method as shown in the video.

Putting a rational expression in its lowest terms (also called "reduction") is a bit tricky, but it becomes very easy once you know a few tricks.

A factoring problem that has to be solved by grouping is easy to identify, because you can always identify if there are any similar terms in a polynomial. Now, if you find any variable common in any terms pull them out as the common leaving the rest of the terms. After pulling out the common terms you can group the rest of the polynomial. Be careful while pulling out signs. Pulling out a positive number does not effect the signs of terms in the polynomial, where as pulling out a negative numb...

In this video, the instructor shows how to factor trinomials. An equation is a trinomial if it has three terms. If you factor a trinomial, you are left with two binomials which are the factors of the original trinomial. Multiplying them would result in the original trinomial. Now factor the last numerical term such that the sum or difference of those factors gives you the numerical coefficient of the middle term. Now split the middle term according to the factors obtained in the previous term...

Multiplying polynomials is a distributive property. If you are given with two binomials and asked to multiply them, you need to apply the distributive property and multiply the terms of binomial with the terms of second binomial. To do this first take a term of first binomial and multiply it with the second complete binomial. Now take the second term of first binomial and multiply it with the second binomial adding or subtracting it from the previous result depending on the sign between the f...

In this video the instructor shows who to simplify radicals. If you have a term inside a square root the first thing you need to do is try to factorize it. First factorize the numerical term. Write down the numerical terms as a product of any perfect squares. Now split the original radical expression in the form of individual terms of different variables. Now you can pull out the perfect square numerical factors out of the radical. Similarly for the variable terms write the variables as power...

In this video the instructor shows how to solve a quadratic equation. If you have a quadratic equation with complex fractional terms and you find that a particular term is repeating then equate that term to a new variable and replace the variable in the given equation. Now try to get the equation a*x*x + b*x + c = 0, and solve for the roots of the equation which gives the values of the intermediate variable. But this variable was replaced instead of another term. So equate that term to the va...

In order to solve a quadratic equation by completing the square, take a quadratic equation and make sure that the coefficient of the first squared term in one. If it is not factor it by pulling the term out to get it to one. Now just write down the first two terms in side a bracket and after it add the third term. Now take the coefficient of the x term and take one half of it and square it and put that number back into the bracket. Now as you added a new number, to cancel it out subtract it f...

If you're serious about playing an instrument well, especially the piano, then you need to know your Italian music terms. Whether you need to play a note staccato or legato or don't recognize what all those tiny abbreviations on your sheet music mean, this tutorial will be a great help in teaching you all the terms you need to know.

This lesson describes the method to find the factors of a trinomial, which consists of three terms, by grouping. First of all, factor out the greatest common factor (GCF), and write the reduced trinomial in parentheses. Let the terms of the trinomial be written in order of exponent of the variable. For example, 3(3X2+2X-8) trinomial is written in the order of variable, with 3(GCF) factored out. Now identify the coefficient of the first and last terms, for example in this case, it is 3 and 8. ...

In this episode learn legal terms like "to sue" "to charge" This video is great for advanced, intermediate, and beginner learning to speak the English as a second language (ESL).

Katherine Miller teaches the secrets of starting your term paper research by using concept mapping method. Use a large sheet of paper and a marker to map out our ideas. First take an example like "Succeeding at college and grades" and write down the factors affecting your goal. The most common factor is money, now write down the things that has an impact on money like jobs, business and loans. The other factors are outside life, health, places for help and study habits. Simultaneously write i...

Factor a trinomial by grouping

This video shows the method to write a logarithm as a sum or difference of logarithms. The square root of the term given is taken out as half according to the rule. Then the numerator and denominator is divided into product of factors. This is broken into the difference of numerator and denominator according to the rule. Finally, the product of factors is expressed as the sum of factors. Now we see the domain of the term. As the term is a square root of the term it should be greater than zero...

The video describes the basic process of multiplying two rational expressions. The problem illustrated in this video involved multiplying rational expressions of monomial terms with integer coefficients. As with the other example problems, we follow the steps of: factoring, canceling, and multiplying. Because these terms are monomials, no factoring is required (but we still state it as a step for similarity to solving other problems). We then find the greatest common divisor for both terms to...

In this tutorial the instructor shows how to factor a trinomial with Greatest Common Factor (GCF) and then how to group it. The first thing you have to do when you want to factor a trinomial is look for the GCF. First factor the numerical coefficients of the terms of the equation. Now separate out the common numerical factor and if any common variable. This leaves you with a binomial to be factored. Now to solve this multiply the numerical coefficients of the first term and the last term and ...

This video is for, the more advanced crocheter. The instructor uses terms and demonstrates stitches that will require a basic understanding of crocheting and an intermediate skill level. The instruction given in this video is very easy to understand. The video quality is clear with a close up shot of the needle and yarn. This allows the viewer, to see how each stitch is done. The instructor does the same step many times. This will allow you to practice the same stitch many times without havin...

In this video the math teacher explains the meaning of the indefinite integral formula in calculus by stating it in terms of antiderivatives. He then shows in general terms how this indefinite integral formula has a related derivative formula, i.e. if the derivative of F(x) is f(x) then the indefinite integral of f(x) is F(x) plus a constant term (C). With this general relationship the teacher takes us through three related examples where he converts a derivative formula to an integral formul...

In this video, the instructor shows how to collect like terms and factorize. When you are given a linear equation, the first thing you do is to try to organize it. Pair up the like terms. Add the numerical coefficients of terms with the same variables. This is called collecting the like terms. In case you see any common factor across all the terms, pull it out and tag it to the parenthesis. In this way, you can factorize the equation. Next, bunch together your like terms and sum them up. The ...

In arithmetic, the simplest expression is far preferred to the long eye-boggling one. Stop making your expressions painful optical illusions by watching this tutorial on how to write rational expressions in the lowest terms.

Multi-Step inequalities are inequalities which take more than one step in solving them. You need to follow a step by step approach in solving these kind of problems. Through there is no general method to solve them you can follow a set of guidelines. First thing you have to do is make sure that only x terms remain on the left hand side of the equation. If there are any other numerical terms add the negative of that term to both the sides of the equation to eliminate it on the left hand side. ...

In this video the instructor shows how to factor a trinomial with negative leading coefficient. Most of the students are confused when they have to factor a trinomial with a negative leading coefficient. But there are many ways to solve these kind of problems as shown in this video. One way you can do is that take out the greatest common factor (GCF) of -1 from the equation. So pulling the -1 gives you the original trinomial with all the signs of the terms changed. Now go on and factor the ne...

This video shows the method to factor a trinomial with a negative sign in the front. The first step is to make the first term positive. This is done by taking the negative sign out. Then we see the middle term of the trinomial. The coefficient of the middle term is a positive one in the example shown. We have to group the coefficient of the first and third term in a way so that the difference is positive one. The appropriate combination is chosen so that this becomes true. In this way the tri...

In this video the instructor shows how to divide rational expressions that contain trinomials. A division containing two fractions can always be turned into a multiplication by multiplying the first fraction by the reciprocal of the second fraction. This way any division can be turned into a multiplication problem and solved easily. Now after you convert the division into multiplication factorize the equations. Now you can factorize the equations by splitting the middle term and grouping it i...

In this video the instructor shows how to solve logarithmic equations. To solve a logarithmic equation, the first thing you have to do is try to get one logarithmic term if possible. To subtract two logarithmic terms use the formula Log (a) – Log (b) = Log (a/b). Now to get rid of logs, perform exponentiation of the base. Exponentiation of the base is raising a number to the power of the logarithmic term where the number is the base of the logarithmic term. Here the value turns out to be the ...

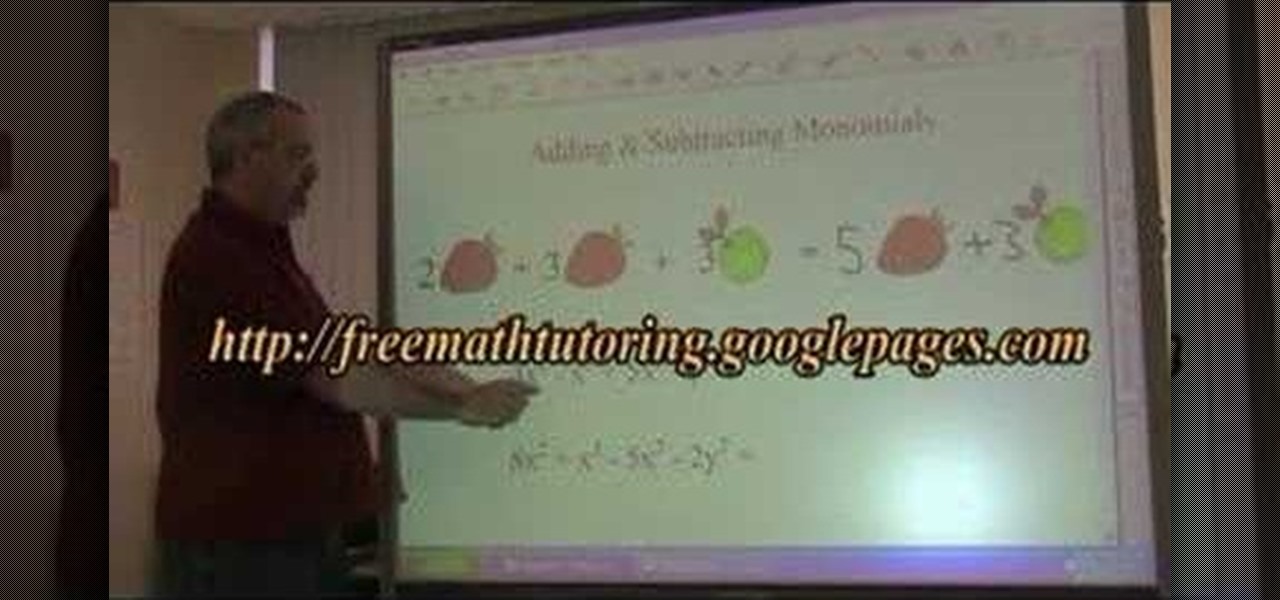
In this video the tutor shows how to add and subtract monomials. He says that to add or subtract monomials they have to be similar terms. Similar terms are those that have same variables and equal exponents to the variables. He shows how to do this using illustrative diagrams and solves a couple of sample problems. He adds a few monomials with similar terms and also explains how to subtract a few monomials. This video gives an introduction to similar terms and how to add and subtract monomials.

The distributive property is a very important factor to consider in math and may save you a lot of trouble on your math homework. For values which lie right outside parentheses, you will need to distribute this value across the contents of whatever is inside the parentheses. You will need to multiply the value outside of the parentheses by first the first term inside the parentheses and then by the following terms inside the parentheses, distributing the value across all the terms found insid...

Like gas on an open flame, rumors and whispers have flared up in recent months around hopes of augmented reality smartglasses from Apple. But among all the false leads and unsubstantiated chatter, we finally have a credible report that some sort of Apple AR smartglasses are actually in development.

Keep Your Word is an innovative and simple Mac application which will let the user keep track of different words - useful for anyone whose area of study gives them a lot of vocabulary words or glossary terms to keep memorized.